The use of Mean is wrong!
The Median and the ideal heel size
Published by Donata Petrelli on 03/06/2021
Reading Time: 3 minutes
It is normal for me, as for many, to buy online and, among other things, yes, even the shoes … with high heels … of course! Not being able to try them on in person, the need arises not to get the size wrong. I do not like to make the return and wait for more time before wearing them J
So … what is the ideal heel size?
I found it, it’s the median of the heel height measurements in my collection!
It has happened to me in the past to buy very low shoes only for practical needs. But these cannot be taken into account when I want to make a new purchase. So I need to eliminate the effects of these extreme values, which are very different from the rest of the data in my collection, to calculate the ideal heel height. This is what the Median does. Let’s see how.
The Median
Given an ordered distribution of values, the median value is the one that occupies the middle position.
The formula for the position of the median is:
where
- N indicates the number of values of the distribution.
Ideal heel calculation
At this point I calculate the median value of the distribution of heel heights in my collection, ordered progressively from smallest to largest. Inserting the values in a sheet of Excel in the cells A2:A23 and using the function
=MEDIAN(A2:A23)
we obtain the value 8 as shown in Figure 1
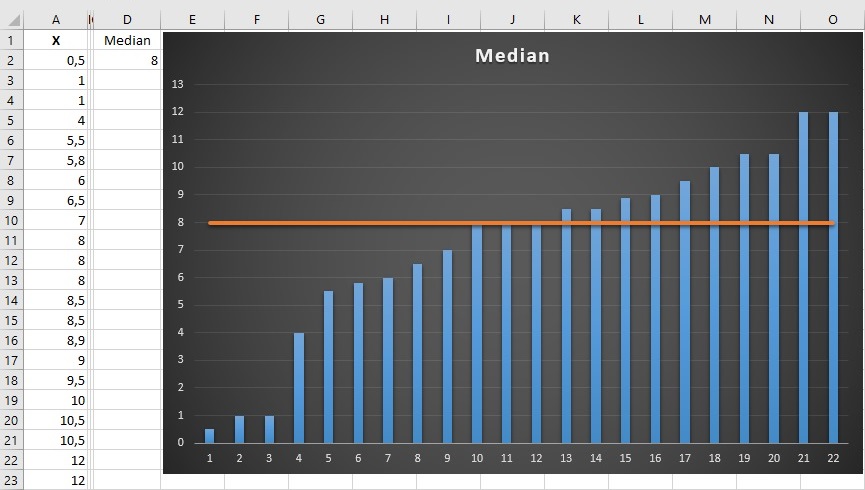
Advantage over Mean
If I had instead calculated the mean heel heights of my shoes using the function
=AVERAGE(A2:A23)
I would have obtained as an indicator of the ideal heel the value 7.3 as shown in Figure 2
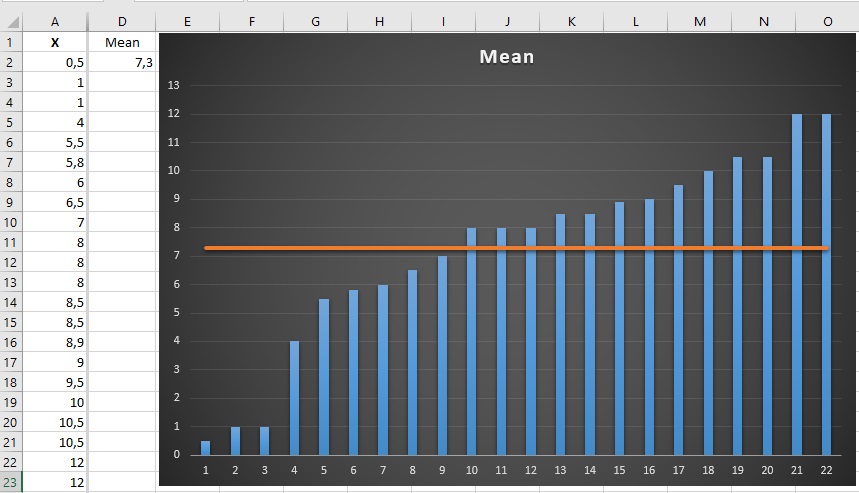
In this case, I would have bought a much smaller size heel!
This is because the mean, unlike the Median, is influenced by the extreme values in this case very different from the rest of the data set.
For you it will not mean much … but for me 1 cm of heel makes a lot of difference J
Conclusion
Normally, the mean is used to have a summary value that describes a set of data. However, the presence of a value much larger or much smaller than the others in the distribution affects this indicator, while it does not change the median.
Whatever the field of application, in our analysis we must often take into account outliers and make sure that their presence does not influence our decisions in a distorted way.
In these cases the Mean is not adequate as it is affected by outliers while the Median is preferable as it is not affected.
With this solution I have never made a single mistake in buying a heeled shoe J
If you found this article useful and want to know about new articles, I invite you to sign up for my blog’s free newsletter.
Published with licenza CC BY-NC-ND 3.0 IT (Creative Common – Attribuzione – Non commerciale – Non opere derivate 3.0 Italia)



