The Black Swan​ Prediction

Predictive mathematical models in “particular” contexts

Reading Time: 6 minutes

Post published on 23/04/2020 by Donata Petrelli and released with licenza CC BY-NC-ND 3.0 IT (Creative Common – Attribuzione – Non commerciale – Non opere derivate 3.0 Italia)

Title Image credits by Chamathe

We are living one of the most complex moments in history that will surely lead to profound changes in our lives. These changes will affect political, economic, social and financial areas and will take place on many levels, many of which will lead to unprecedented events. Some are already happening, such as what is happening with the price of oil falling to negative values for the first time in history. Apparently it is a non-intuitive concept and to give an example it is as if I went to the baker and he paid me to take my bread away.

Explaining what happened to crude oil is not the purpose of this article, not least because these days there is a lot of talk about it everywhere. For those who want to know more about the problem I suggest reading the excellent article by Business Insider at https://it.businessinsider.com/che-cosa-e-successo-davvero-al-prezzo-del-petrolio/. What I want to deal with in this short article is what I’m often asked in this period, that is how a predictive mathematical model interacts in the presence of an unexpected event or, better, how a predictive model behaves in the presence of “the black swan”.

This article was created in order to give an answer to all those who are asking me. To do this I will try to explain it in simple terms, without using technical terms or, even less, mathematical formulas but I always encourage you to go deeper into the subject both here in the comments and in private.

Predict the unpredictable

One of the biggest problems for us mathematicians is the famous “black swan” prediction. How many times have we been asked if the mathematical model was able to predict an unexpected event which, precisely because of its etymology, is not likely but which, in times of pandemic, becomes as obligatory as the airbag in cars?

This happens because after the occurrence of the unexpected event, which has relevant effects in many fields, it is rationalized and, in an inappropriate way, judged predictable. In spite of this psychological distortion, called cognitive bias, however, a forecasting mathematical model must take those significant anomalies in behavioural patterns considered ordinary before the occurrence of these very rare events.

To give an example in reality, even if it is not possible to know the exact moment of the occurrence of an earthquake of high intensity and devastating effects, in Japan houses are earthquake-proof and as such must resist these earthquakes and have common characteristics such as being quickly accessible.

In the same way, even if it is not possible to predict the occurrence of a very rare event, a mathematical forecasting model must have all those characteristics such that security standards are met. First of all, not to process results always and in any case, but to anticipate a sort of ‘block’ so as not to generate outputs that would cause more damage than the same unpredictable event. Excluding any inadmissible blockages in a given system, it could however enter into some kind of security mode. Let us think, for example, of a financial Robo that did not take into account the current anomaly of the oil trend and continued to manage its portfolios in conditions of regime. Let’s think of the control unit of a car that, in the event of an anomaly, signals the fault and calls for urgent intervention. If the problem is very serious it goes into reduced mode or even could stop the vehicle, thus avoiding further damage or potential accidents.

Even if a rare event is not predictable, a mathematical model must still be able to ‘defend itself’ from its. But how does it do that? Through its ICT implementation or Algorithm.

A mathematical model and the algorithm of the model are closely related, one cannot do without the other and vice versa. Only their combination makes the final product (software, service or machine that it is) powerful and can therefore also protect us from “the black swan”. Let’s take a closer look at how they work and we will understand it.

Mathematical Model

A mathematical model is the representation, logical and simplified, of a very complex real system. For its creation, it must take into account the parts (parameters) that will constitute it, the relationships that exist between these parts and finally arrive at the final prediction of the results. Then how it does, it determines whether it is a valid model or not.

A model is supported by test results. I would like to summarise its functionality with a picture, since that is not the purpose of the article. However, for those who want to know it in detail, you can read an entire chapter in the book “Excel and Artificial Intelligence for Trading” (https://www.donatapetrelli.com/books/) from which the explanatory image is taken

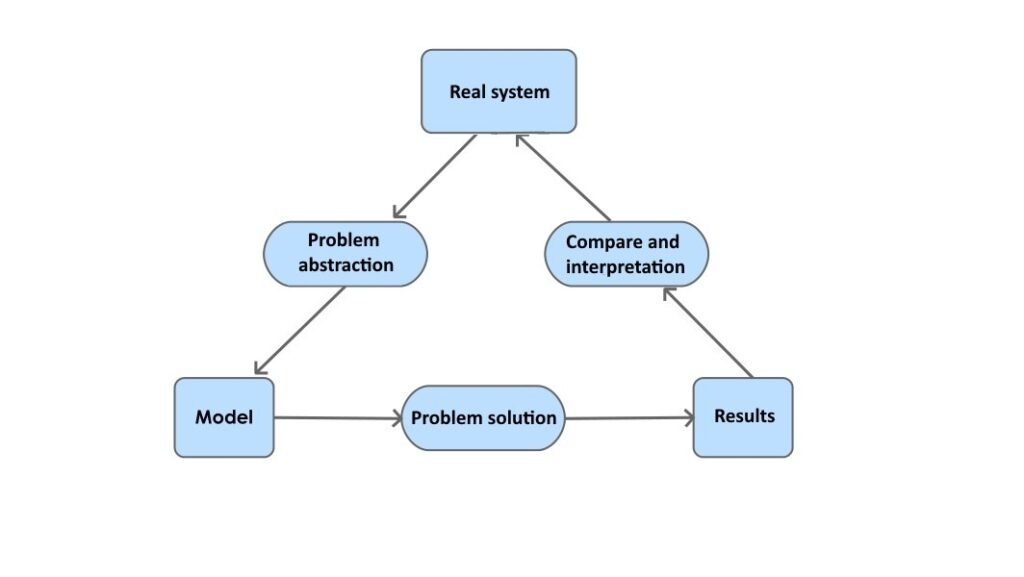
There are indicators that measure its accuracy:

• the goodness, i.e. how well it describes reality
• the strength, which is how much I can trust the results in the forecast

These aspects of the model, although very interesting, go beyond the context of this article, and they deserve to be explored separately. What interests us to know is that it is possible to evaluate the accuracy of the model and to understand how much we can trust its results for our future decisions.

You may have noticed that, until now, the rare event has not yet been taken into account. In other words, we can say that the ultimate goal of the mathematical model is prediction only.

The Algorithm

By definition, an algorithm is a process that solves a given problem through a finite number of elementary, clear and unambiguous instructions. The algorithm is therefore entrusted with the task of managing all the possible events and combinations between them.

It is during the elaboration of the algorithm that an unpredictable event is taken into consideration or, in any case, it is the task of the algorithm to verify that there are anomalies that change the normal behaviour of the events taken into consideration.

In this case the algorithm must manage the anomaly. There are several ways to do this by raising a meaning, sending/displaying an alarm message that prevents the normal running of the program but makes you think about what to do, entering a particular execution mode or any other way useful for the purpose. In the example of the Financial Robo, if the model is not expected to work in rare conditions such as that of the negative price of a asset, it must be the task of the algorithm to warn when you are close to zero and “stop the engine”.

All this happens because the true mathematical forecasting model is implemented in an algorithm, as described in the following scheme:

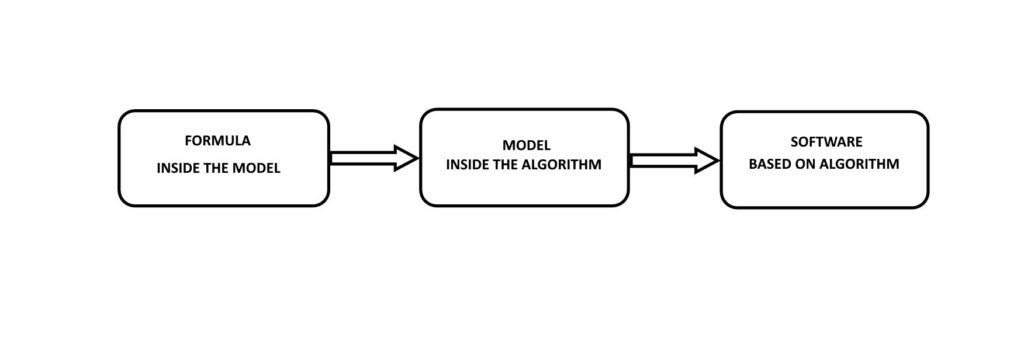
In programming there are various event management and code control tools and many design, development and testing techniques such as Unit Test and Stress Test to name but a few. These techniques allow you to quickly detect vulnerabilities and malfunctions and test a wide variety of cases. Also in the financial domain we can use specific tools whose purpose is to perform a simulation of a certain operation to evaluate possible future operational decisions.

The important thing is that those who implement the algorithm anticipate the unpredictable in order to get a robust code. Precisely for this reason, for some time now, I use a simulator created ad hoc that can test any situation or future scenario.

Conclusion

In reality, therefore, the mathematical model is the fundamental part, the heart of the system, but it does not complete itself. The algorithm that ‘encapsulates’ it and all the techniques we have mentioned make the system powerful. To make a comparison if the mathematical model is the brain, the algorithm and the control techniques are the parts of the body (eyes, limbs, mouth, …) that are able to externalize and control the impulses of the brain. This is why the mathematical model and algorithm are interdependent.

Finally, we must take into account that the whole final system {model+algorithm} must be contextualized in one environment. This means that if the same one is valid and gives high performance for a certain environment, used for another one it is no longer able to give the same performance and get the same excellent results.

This makes the discussion even more complex … after all, as the great George Edward Pelham Box said …

“All models are wrong, but some are useful”